Turning Points

• deepak.c

  23 Apr 09, 05:43

   

  f(x) = 2 sin x + cos 2x

   

  f'(x) = 2 cos x - 2 sin 2x

   

  How many methods are there to find the turning points from 0° to 360°?

   

  Thanks to all those who took an effort.

   

• wee_ws

  23 Apr 09, 08:51

  Hi,

    For stationary points, f'(x) = 0, i.e. 2 cos x - 2 sin 2x = 0.

    Then cos x = sin 2x

    => cos x = 2 sin x cos x

    => (cos x) (2 sin x - 1) = 0

    => cos x = 0 or sin x = 1/2

    ...

    Try it, thanks!

  Cheers,
  Wen Shih 

• deepak.c

  23 Apr 09, 10:03

   

  Don't quite understand the answer, anyway I managed to plot the graph from 0° to 360°.

  Thanks.

  

• eagle

  23 Apr 09, 10:07

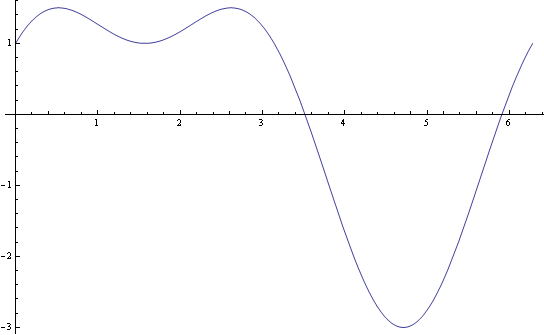
  hi

  Mr Wee means to use the first derivative, f'(x), and equate it to zero, to find stationary points. This is because for stationary points, the gradient of the graph at that point is zero.

  Which part of his answer do you find hard to understand? Perhaps you can list it out :D

   

• deepak.c

  23 Apr 09, 10:19

   

  If cos x = 0, means 90° is one of the turning points, when substituted back into f'(x), you get zero.

  e.g. 2 cos 90° - 2 sin 180° = 0

  But sin x = 1/4, means 14.4775°, when substituted back into f'(x), does not equate to zero. There are still 3 turning points left after 90°.

   

• deepak.c

  23 Apr 09, 10:27

   

  I think I got it, there was a careless mistake with Mr. Wee's double angle formula.

   

  Thanks.

   

   

• deepak.c

  23 Apr 09, 10:35

   

  Double-Angle Formula:

  sin 2x = 2 sin x cos x

   

  f'(x) = 2 cos x - 2 sin 2x = 0

  ==> 2 cos x - 2 (2 sin x cos x) = 0

  ==> 2 cos x (1 - 2 sin x) = 0

   

  cos x = 0 (90, 270) and sin x = 1/2 (30, 150)

  The other 2 points are reference angles.

   

  Thanks.

   

• wee_ws

  23 Apr 09, 12:10

  Hi,

    Good observation!

  Cheers,
  Wen Shih

• HiAy3Captain

  23 Apr 09, 13:09