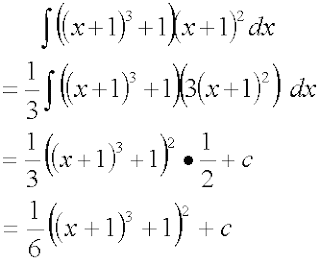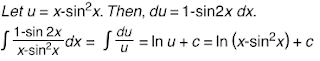integration questions

• xstryker

  13 May 09, 19:27

  i just read some of examworld's integration questions and dont really get some of the steps in the answers.

  (1) Integrate [(x + 1)³ + 1](x + 1)²

   

  
  

  um where did the 1/3 and the 3 come from?

   

  and (5) Integrate (1 - sin2x)/(x - sin² x)

   

  

  someone mind explaining?

• deepak.c

  13 May 09, 20:08

   

  y = (x + 1)^3

  dy/dx = 3(x + 1)^2

   

  The 3(x + 1)^2 is the derivative of (x + 1)^3, you just need to prefix a "3" in front, so to cancel out the 3, you do a 1/3.

   

   

   

• deepak.c

  13 May 09, 22:27

   

  Differentiation product rule, chain rule also can :

  u = x - (sin x)^2

  u' = 1 - 2 sin x cos x

  u' = 1 - sin 2x ===>>> (sin 2x = 2 sin x cos x) aka double angle formula

   

  Integrate [1/u] du = ln u + c (I cannot do the integral sign)

   

  Then all you have to do is slot in "u" into "ln u + c":

  ===>>> ln (x - (sin x)^2) + c

   

  I just learnt this just now.

   

   

• eagle

  13 May 09, 23:32

  thanks for helping to explain

   

  Am glad something new is learned :D

• deepak.c

  15 May 09, 07:19

   

  Just realised that there is something wrong with your answer for question 2.

   

  It should be ln |x - (sin x)^2| + c

   

  It should be the absolute value.