Plane geometry (urgently need help!)

• bonkysleuth

  20 May 09, 17:24

  The diagonals of cyclic quadrilateral PQRS intersect at U. The circles's tangent at R meets PS produced at T. If QR = SR, prove that

  PR x ST^2 = UR x RT^2

   

  Haven't been able to sovle this ever since my MYE. Can someone help?

   

• Forbiddensinner

  20 May 09, 20:46

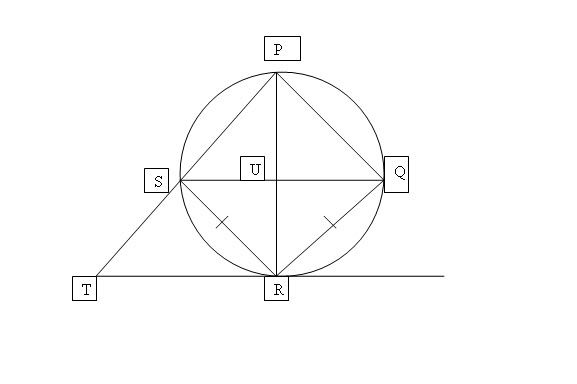
  Originally posted by bonkysleuth:

  The diagonals of cyclic quadrilateral PQRS intersect at U. The circles's tangent at R meets PS produced at T. If QR = SR, prove that

  PR x ST^2 = UR x RT^2

   

  Haven't been able to sovle this ever since my MYE. Can someone help?

   

  After 2 hours of work...I finally got a random guess answer which is most likely partially wrong, but can be used to work towards the correct answer.

  Things you need to know:  PR = RT,  PSU AND PTR are similar triangles.

  UR / PR = ST / PT

  UR / PR = (ST)^2 / (PT)(ST)

  UR / PR = (ST)^2 / (PT)(PT - SP)

  UR / PR = (ST)^2 / (PT^2 - (PT)(SP))

  UR / PR = (ST)^2 / (PT^2 - (1/2(PT) X (PT)))

  UR / PR = (ST)^2 / (PT^2 - (1/2)(PT^2))

  UR / PR = (ST)^2 / (1/2)(PT)^2

  UR / PR = (ST)^2 / (1/2)((RT)^2 + (RP)^2)

  UR / PR = (ST)^2 / (1/2)((RT)^2 + (RT)^2)

  UR / PR = (ST)^2 / (RT)^2

  PR X (ST)^2 = UR X (RT)^2

  Discuss any mistakes you find in my workings.

   

• eagle

  20 May 09, 20:56

  edit: answer already above

• eagle

  20 May 09, 21:38

  ok finally got some time to take a look

  this is what I would do

  angle RSQ = angle SQR (isos)
  angle SQR = angle SRT (alt. segment)
  Hence angle RSQ = angle SQR
  ==> SQ is parallel to RT
  ==> PSU and PTR are similar triangles

   

  Using tangent secant theorem,
  ST * PT = RT^2 ------------------- (1)

  Using intercept theorem,
  PS / ST = PU / UR
  PS / PU = ST / UR
  
  Also,
  PS / PU = PT / PR (similar triangles)
  

  Hence,
  PT / PR = ST / UR
  PT = ST * PR / UR ---------------------- (2)
  
  Sub (1) into (2)
  ST^2 * PR / UR = RT^2
  PR x ST^2 = UR x RT^2 (shown)

• eagle

  20 May 09, 21:46

  ***********************************************************************************************

  wait... on second thoughts, after looking at Forbiddensinner's solution, I can combine our solutions together to become an even shorter solution

  After proving the similar triangles,

  Using intercept theorem,
  UR / PR = ST / PT
  UR / PR = ST^2 / (PT)(ST)

  Using tangent secant theorem,
  ST * PT = RT^2

  Hence,
  UR / PR = ST^2 / RT^2
  PR * ST^2 = UR * RT^2