Kinematics

• Jt061952

  28 May 09, 12:49

  Please help check this kinematic problem:

   

  A particle P travels in a straight line from a fixed point O such that its acceleration, a m/s2, is given by a = 6t + k, where t is the time in seconds after it passes O and k is a constant.  If the velocity of P is -16 m/s after 1 second and P comes to instantaneous rest after 5 seconds,

  i)   find the value of k

  ii)  find the distance travelled in the first 6 seconds.

   

  Integrate a = 6t + k

                 v = 3t^2 + kt + c

              -16 = 3 + k + c

              -19 = k + c  .........(1)

   

                 0 = 75 + 5k + c ..(2)

   

  Solving both eq, I got k = -14 and c = -5

   

                 v = 3t^2 -14t -5

   

  For part (ii) I integrate  v = 3t^2 - 14t -5 from 5 to -1 (??) is this right and got 72 m.  Answer in paper says 84m.  Thanks for helping.

   

   

   

   

• deepak.c

  28 May 09, 14:29

   

  Plot the graph 3t^2-14t-5 on your graphical calculator (t = -2 to 8)

   

  You would need to integrate from [5, 0] = 75 and [5, 6] = 9

   

  

• wishboy

  28 May 09, 20:46

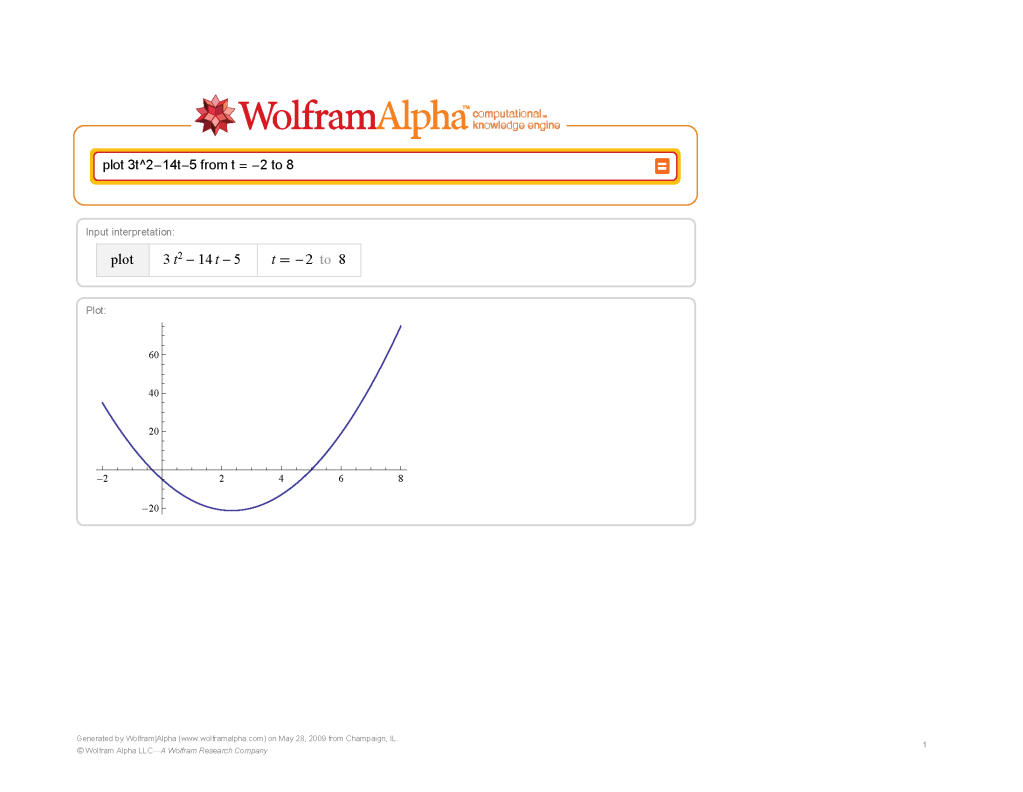
  Originally posted by Jt061952:

  For part (ii) I integrate  v = 3t^2 - 14t -5 from 5 to -1 (??) is this right and got 72 m.  Answer in paper says 84m.  Thanks for helping.

  Integrate from 5 to 0 (t = 5 is a turning point of the graph as P is at instantaneous rest)

  Also, integrate from 6 to 5 to find distance travelled from t = 5 to t = 6.

  Add this 2 values together

• Jt061952

  29 May 09, 06:46

  Thanks.  I thought since it came to an instantaneous rest at 5 sec, I don't integrate beyond 5 sec.  Appreciate it.