A maths question - trigo

• bonkysleuth

  3 Jun 09, 21:31

  

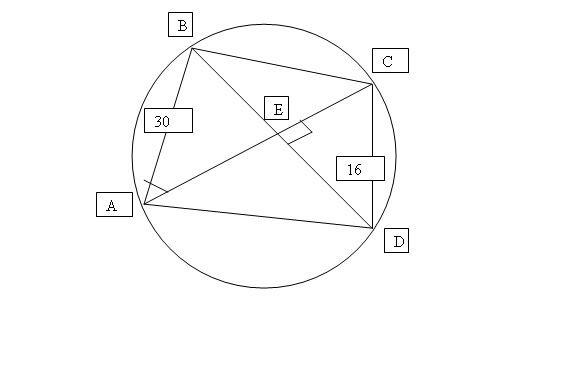
  The diagram shows that A, B, C and D are 4 points on the circumference of a circle where AB = 3 cm , CD = 16 cm and angle BA = titer (the 0 with a line in the middle,haha). AC and BD are perpendicular to each other at E. Show that the are of the quadrilateral ABCD is (289 sin 0 + 240) cm2

  take note that the 0 beside the "sin" is referring to titer or deteer or whatever. thanks.

• wee_ws

  4 Jun 09, 05:41

  Hi,

    I think there is a typo error in the expression to be proved, as I obtained 289 sin 2(theta) + 240. Also, AB = 30 cm as shown on the diagram but it is written as 3 cm in the problem statement.

    The approach:

    1. angle ABE = angle CDB = theta (angles in the same segment).

    2. From triangle ABE: AE = 30 cos (theta), BE = 30 sin (theta).

    3. From triangle CDE: DE = 16 cos (theta), CE = 16 sin (theta).

    4. Area = area of triangle ABC + area of triangle ADC

                  = 1/2 (30 cos theta + 16 sin theta)(30 sin theta) +

                     1/2 (30 cos theta + 16 sin theta)(16 cos theta).

    5. Expand and simplify to 289 sin 2(theta) + 240.

    Thanks!

  Cheers,
  Wen Shih

• bonkysleuth

  4 Jun 09, 19:14

  Originally posted by wee_ws:

  Hi,

    I think there is a typo error in the expression to be proved, as I obtained 289 sin 2(theta) + 240. Also, AB = 30 cm as shown on the diagram but it is written as 3 cm in the problem statement.

    The approach:

    1. angle ABE = angle CDB = theta (angles in the same segment).

    2. From triangle ABE: AE = 30 cos (theta), BE = 30 sin (theta).

    3. From triangle CDE: DE = 16 cos (theta), CE = 16 sin (theta).

    4. Area = area of triangle ABC + area of triangle ADC

                  = 1/2 (30 cos theta + 16 sin theta)(30 sin theta) +

                     1/2 (30 cos theta + 16 sin theta)(16 cos theta).

    5. Expand and simplify to 289 sin 2(theta) + 240.

    Thanks!

  Cheers,
  Wen Shih

  
  Thanks  wee_ws! My approach to this question was the same as yours. But unfortunately, the only difficulties I have is "Expand and simplify to 289 sin 2(theta) + 240.". I tried but I just can't transform the equation to the above. That's what initially led me to think that I might have done it incorrectly. Is there some way to reduce it to 289 sin 2(theta) + 240.?

   

• wee_ws

  4 Jun 09, 22:46

  Hi,

    Area = 1/2 (30 cos theta + 16 sin theta)(30 sin theta) +

                 1/2 (30 cos theta + 16 sin theta)(16 cos theta)

    = 450 sin theta cos theta + 240 sin^2 theta

       + 240 cos^2 theta + 128 sin theta cos theta

    = 240 + 289 (2 sin theta cos theta)

    = 240 + 289 sin 2 theta.

    Thanks!

  Cheers,
  Wen Shih

• anpanman

  5 Jun 09, 03:01

  This's quite a useful thread. Frankly speaking, I myself do not think of the equation being about to be multiplied in such a way. I only thought of factorising it.(since most of the times we are told to factorise to not "complicate" equations! Haha)

   

  Thanks wee_ws and bonkysleuth!

• wee_ws

  5 Jun 09, 08:11

  Hi,

    Welcome :)

    Singapore-style mathematics is really very challenging at times :P

  Cheers,
  Wen Shih