H2 summation question

• Occam's Razor

  5 Jun 09, 17:11

  Hi, I was doing my revision questions and bump into some problems on summation.

  ^Im not sure how to prove the second part.
  
  ^ Not sure how to explain (iv)
  
  Thanks.

• Forbiddensinner

  5 Jun 09, 21:13

  Originally posted by Occam's Razor:

  Hi, I was doing my revision questions and bump into some problems on summation.

  ^Im not sure how to prove the second part.
  
  ^ Not sure how to explain (iv)
  
  Thanks.

  For the 1st one, I will type it out in words.

  Since the 1st part has been proven,

  Summation 1/ ( Square root r + square root (r-1) ) = square root n

  One thing you must realise is that the bigger the denominator, the smaller the value.

  Since ( 2 square root r ) is bigger than ( square root r + square root (r-1) ), the summation of 1/ (2 square root r ) must be smaller than the summation of               1/ ( Square root r + square root (r-1) ), hence the summation of 1/ (2 square root r ) must be less than square root n.

   

  For the 2nd one, (iii) shown that when x is between 0 and 1, the next number in sequence will be larger than the previous one. (iv) also shown that f(x) is increasing between - (square root 3) and (square root 3). 

  Hence, this shown that x = 0.5, which is in (ii), will increase ( even if you do not calculate it out ), as 0.5 lies well within the requirements shown in (iii) and (iv).

  In short, (iii) and (iv) shown what will happen in (ii).

   

  I have always been lousy when it comes to putting such stuffs into proper sentences, so you will have to think about it for a while.

   

   

• wee_ws

  5 Jun 09, 22:59

  Hi,

    Your explanations are clear enough, so do congratulate your effort :)

  Cheers,
  Wen Shih

• Occam's Razor

  5 Jun 09, 23:03

  Ok thanks! :)
• eagle

  6 Jun 09, 01:24

  first question appeared in 2006 TPJC J1 Common Test :D

• Occam's Razor

  12 Jun 09, 15:31

  Hi, I have another question I'm stuck with.

  Im not sure about the last part.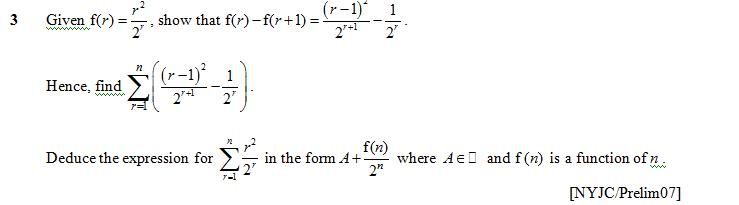
• wee_ws

  12 Jun 09, 17:25

  Hi,

    When the question asks one to deduce, it means that the new summation can be expressed in terms of the original.

    One practical strategy is to expand the new summation and see clearly how it is related to the original.

    Note also that the sum of 1/2^r is a sum of GP.

    Try it. Thanks!

  Cheers,
  Wen Shih

• Occam's Razor

  12 Jun 09, 22:09

  Hi, I tried that method and came to a dead end.
  
  

• wee_ws

  12 Jun 09, 22:36

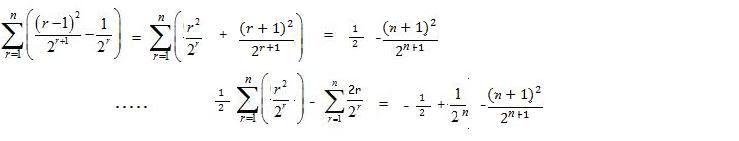
  Hi,

    sum {1, n} [ (r - 1)^2/2^(r + 1) - 1/2^r ] = f(1) - f(n + 1), by the method of differences.

    So sum {1, n} (r - 1)^2/2^(r + 1) = f(1) - f(n + 1) + sum {1, n} 1/2^r.

    Now sum {1, n} (r - 1)^2/2^(r + 1) can be expanded into

    0/2^2 + 1^2/2^3 + ... + (n - 1)^2/2^(n + 1), which can be re-expressed as

    1/2^2 [ 1^2/2^1 + 2^2/2^2 + 3^2/2^3 + ... + (n - 1)^2/2^(n - 1) ] -- (1).

    The new sum is sum {1, n} r^2/2^r, which can be expanded into

    1^2/2^1 + 2^2/2^2 + ... + n^2/2^n -- (2).

    Comparing (1) and (2), we see that

    sum {1, n} r^2/2^r = 2^2 sum {1, n + 1} (r - 1)^2/2^(r + 1) yes?

    Thanks!

  Cheers,
  Wen Shih

• Occam's Razor

  12 Jun 09, 23:03

  Oh ok, never thought of doing it this way. Thank you very much :)

• wee_ws

  13 Jun 09, 12:34

  Hi,

    That was what I meant by expansion :)

    This strategy always works, because we can see patterns through concrete numbers. Thanks!

  Cheers,
  Wen Shih

• wee_ws

  13 Jun 09, 19:24

  Dear students,

    I have written a detailed article on the handling of summations which may be helpful in your problem-solving:

    http://www.freewebs.com/weews/sequencesseries.htm

    Thanks!

  Cheers,
  Wen Shih