E maths - Few questions
-
The cumulative frequency curve below shows the time Mr Smith takes to travel to work over 300 days. What is the estimate of the probability that his journey takes more than 25 minutes on 1 day and less than 25 minutes the next day?
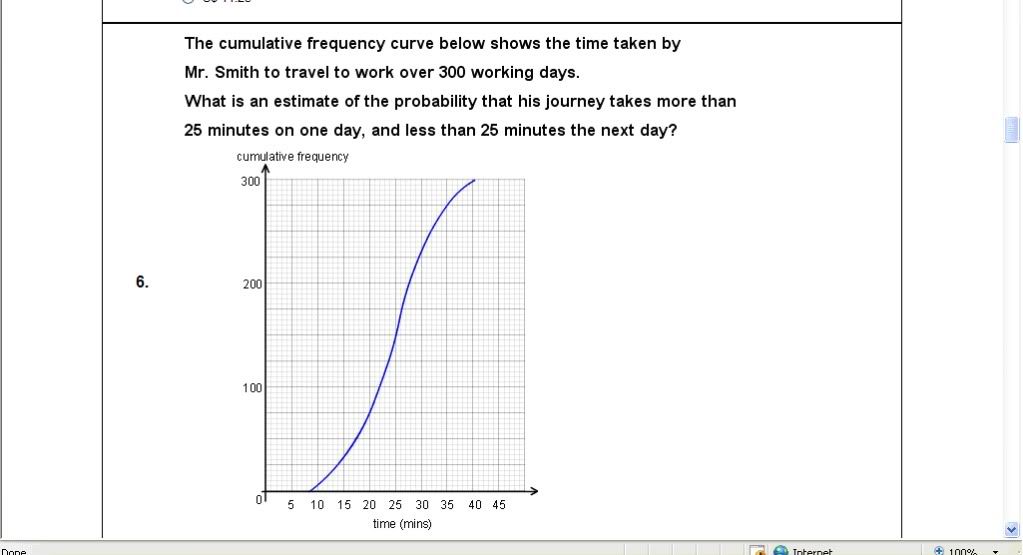
Whether it's less than 25 or more than 25 minutes both are at 150 days. So I used 150/300 X 150/299?? Seems to get the wrong answer. May I know where I went wrong?
2. In a family of 5, the probability sue reaches home first is 7/12 and probability joe reaches home first is 1/12. Find the probability that either sue or joe is first home. My answer to to just add the 2 values together. Just to double check, is it right?
3.
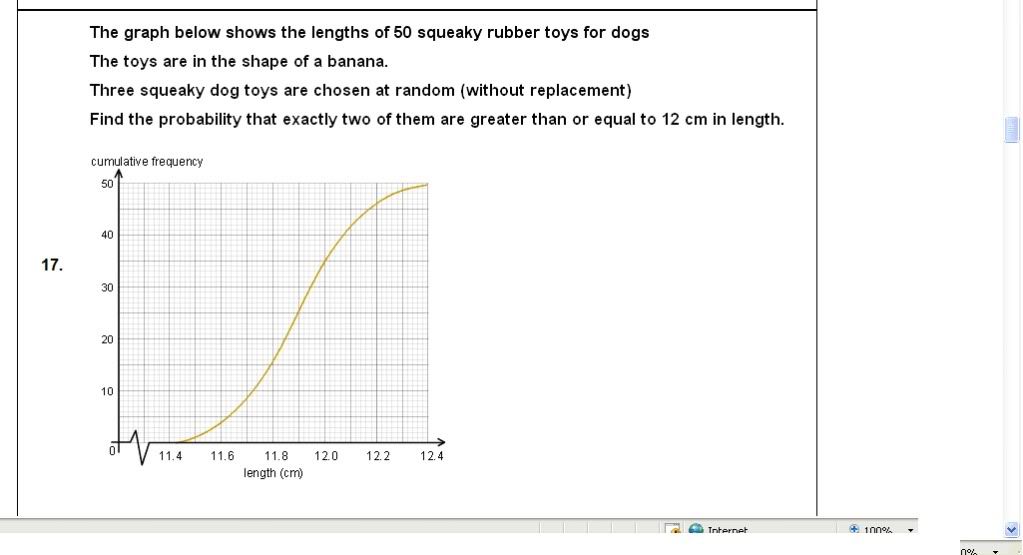
Here's what I did.
3 X (15/50 X 14/49 X 35/48) = 3/16
Is my answer correct? I multiplied by 3 because the dogs couldbe chosen in the following orders. X represents more than 12 cm while y reps less than 12cm.
( x,x,y) (y,x,x),(x,y,x)
thanks
-
u got the correct answers right? post it here also, easier for ppl to check mar : )
-
Originally posted by MasterMoogle:
u got the correct answers right? post it here also, easier for ppl to check mar : )
Nope I don't. I only have a selection of answers. 4 options. Unless you want me to provide the 4 options? Needa take some time. Will most likely post the options tomorrow. (: -
just guesswork here btw (threw my probability stuff out a long time ago)
1. shouldn't it be 150/300 * 150/300 = 1/4? seeing that his travel time on day X doesn't affect day X+1
2 & 3. sounds right...
-
Originally posted by ThunderFbolt:
just guesswork here btw (threw my probability stuff out a long time ago)
1. shouldn't it be 150/300 * 150/300 = 1/4? seeing that his travel time on day X doesn't affect day X+1
2 & 3. sounds right...
But why is it that you multiply it by 150/300 again? I thought that after having travelled one day, the total number of days for the travel has decreased by 1 so shouldn't you use 299 instead? Thanks anyway -
because regardless of the day he still has a 50% chance of arriving before 25 mins. the graph doesn't show day 1, this happens, day 2, this happens and so on.
btw, this is what i think only. hoping someone else also come give their take on the question.
-
Originally posted by ThunderFbolt:
because regardless of the day he still has a 50% chance of arriving before 25 mins. the graph doesn't show day 1, this happens, day 2, this happens and so on.
btw, this is what i think only. hoping someone else also come give their take on the question.
yes, i also agree
-
Hi,
Probability is indeed (1/2)(1/2) = 1/4. Thanks!
Cheers,
Wen Shih