A maths (trigo questions)
-
An isoceles triangle RST with RS = RT is inscribed in a fixed circle with centre O. The radius of the circle is 4 cm and angle SOT is 2 theta where theta is acute and measured in radians
Show that the area A cm^2 of the triangle RST is given by A = 16 sin theta + 8 sin 2 theta
Hence show that as theta varies, when the triangle RST is equilateral, triangle RST has a maximum area.
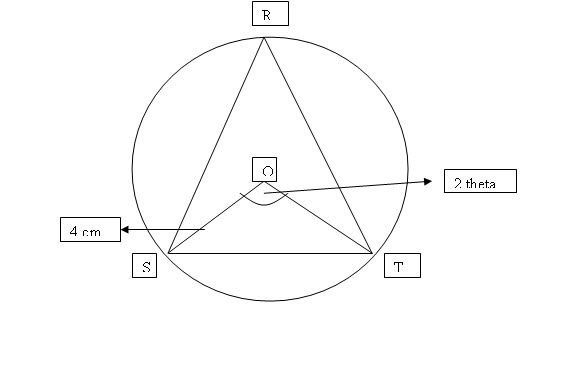
I have problems with the final part. Can someone help me out with this? thanks
-
A=16sin x + 8 sin 2x
dA/dx = 16cos x + 16 cos 2x
When dA/dx = 0
16cos x + 16 (2 cos^2 x -1) = 0
2cos^2 x - cos x -1 =0
(2cos x -1)( cos x + 1)=0
cos x = 1/2 or cos x = -1 (NA)
x = pi/3
theta is pi/3 and the other 2 angles same
Angles OST and OTS = pi/3
d^2A/d^2x = -16sinx - 32cos 2x
When x = pi/3
d^2A/d^2x = -ve (Max)
Therefore... blah blah blah
Done
-
H Mikethm, I tried out your method by d^2A/dx^2 is positive not negative... Thanks anyway. ^^
-
There's a careless mistake
should be
d^2A/d^2x = -16sinx - 32sin 2x
You should be able to do now :D
-
ya had a typo. differentiate 16 cos 2x would be -32sin 2x. Thanks.