E maths - vectors
-
the diagram below shows a paralleloram OABC. O is the origin, A is the point (4,2) and vector AB = (-12 3) and vector AK = 1/3 vector AB. The lines AC and OK intersect at point T. Find
The numerical value of area of triangle AKT/ triangle OCT
Previous questions before this were: Find position vector of K and the numerical value of area if triangle OAK/ trrangle OBK
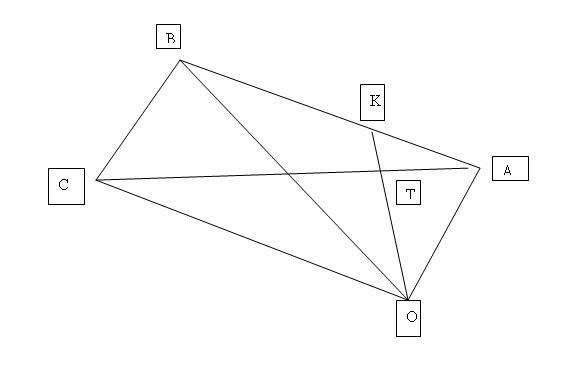
PS the highlighted parts are supposed to be written in column vector form.
-
Another question. Not related to vector.
The figure shows 2 circular tops spinning at the same time. They are connected by 2 straight wires AB and CD. The tops have centres A and B with radii 7 cm and 5 cm respectively. CD is a common tangent to the circular tops. It is given that AB = 15cm.
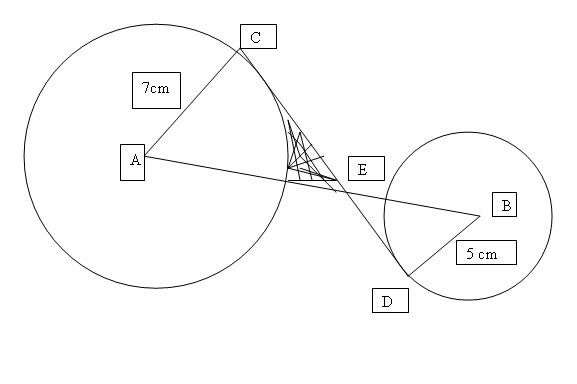
Stating your reasons, how that the length of AE - 8.75cm. Hence find the length of CD.
Answer for CD = 9 cm
-
Originally posted by anpanman:
the diagram below shows a paralleloram OABC. O is the origin, A is the point (4,2) and vector AB = (-12 3) and vector AK = 1/3 vector AB. The lines AC and OK intersect at point T. Find
The numerical value of area of triangle AKT/ triangle OCT
Previous questions before this were: Find position vector of K and the numerical value of area if triangle OAK/ trrangle OBK

PS the highlighted parts are supposed to be written in column vector form.
AB = OC, as OABC is a parallelogram.
Hence, AK = 1/3 OC
Looking carefully at triangle AKT and triangle OCT, you will realise that both of them are similar triangles.
Hence, area of AKT/ area of OCT = (AK/OC)^2 = (1/3)^2 = 1/9
-
Originally posted by anpanman:
Another question. Not related to vector.
The figure shows 2 circular tops spinning at the same time. They are connected by 2 straight wires AB and CD. The tops have centres A and B with radii 7 cm and 5 cm respectively. CD is a common tangent to the circular tops. It is given that AB = 15cm.

Stating your reasons, how that the length of AE - 8.75cm. Hence find the length of CD.
Answer for CD = 9 cm
AEC and DEB are similar triangles.
DB / AC = BE / AE ------- 1.
AE + BE = 15cm = > BE = 15cm - AE -------- 2.
Put them together, and you will get,
5 / 7 X (AE) = 15cm - AE
AE = 8.75cm
CED is a tangent to both circles, so angle ACE and angle EDB are 90 degrees.
CE = sqrt ( (AE)^2 - (AC)^2 )
ED = sqrt ( (ED)^2 - (DB)^2 )
CD = CE + ED = 9cm