Vectors - e maths
-
In the diagram , OA is parallel to CB and SC is parallel to AB. The position vectors of A and B relative to O are 4a and 5b respectively. OS/SB = 2/3 and vector AT = 1/4 vector AB
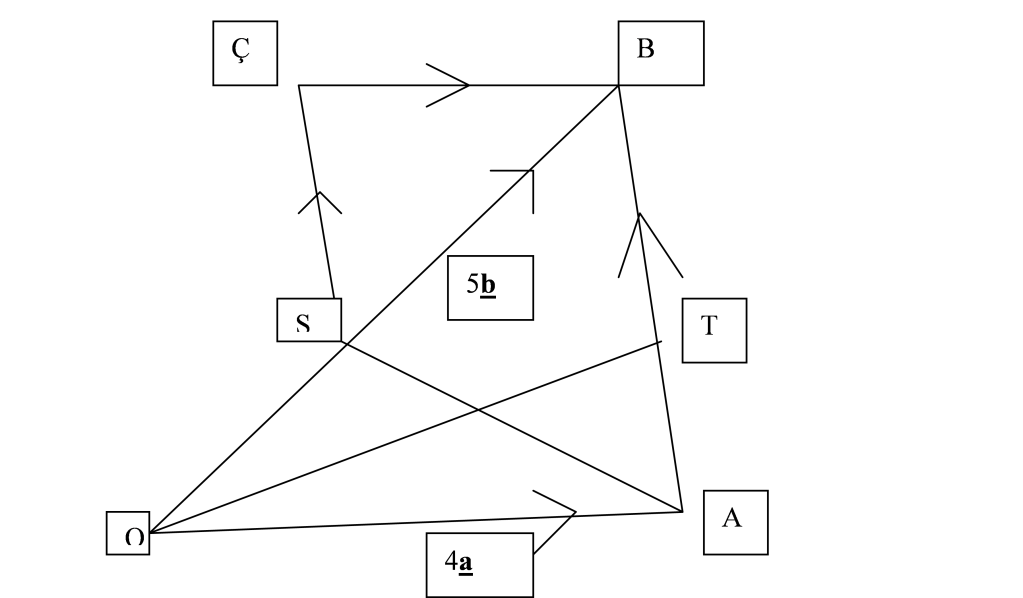
(a)Given that |vector AB| = 15 units, find |vector CS|
write down the ratio of area of triangle SBC/ area of triangle BOA. Ans: 5/8
For this part i made use of the similar triangle fact (CSB and ABO) and managed to get CS = 9 units. but I think my ans for the ratio of area is wrong, didn't get 5/8 but i remember doing this (9/15)^2.
(b)Find the area of triangle OTA/area of triangle OSA
thanks. (urgent, would be good if solutions are up by 6 am tomorrow.)
-
Originally posted by anpanman:
In the diagram , OA is parallel to CB and SC is parallel to AB. The position vectors of A and B relative to O are 4a and 5b respectively. OS/SB = 2/3 and vector AT = 1/4 vector AB

(a)Given that |vector AB| = 15 units, find |vector CS|
write down the ratio of area of triangle SBC/ area of triangle BOA. Ans: 5/8
For this part i made use of the similar triangle fact (CSB and ABO) and managed to get CS = 9 units. but I think my ans for the ratio of area is wrong, didn't get 5/8 but i remember doing this (9/15)^2.
(b)Find the area of triangle OTA/area of triangle OSA
thanks. (urgent, would be good if solutions are up by 6 am tomorrow.)
5/8 is the answer for part (b).
Your part (a) answer should be 9/25.
AB = 5b-4a
AT= (1/4)[5b-4a]
Since SC/AB = 3/5, perpendicular line from OA to S = 2/5 AB, which is (2/5)[5b-4a]
Area = 1/2 X base X height
Area of OTA = 1/2 X 4a X (1/4)[5b-4a]
Area of OSA = 1/2 X 4a X (2/5)[5b-4a]
Area of OTA/Area of OSA = (1/4) / (2/5) = 5/8