E maths - Cylinder question
-
Diagram 1 shows a cylindrincal tank of radius 50 cm and length 120 cm. The tank is partially filled with water and placed with its curved surface on a horizontal floor.
Diagram II shows the circular cross-section of the cylinder. O is the centre of the circle. Angle AOB = 2 radians
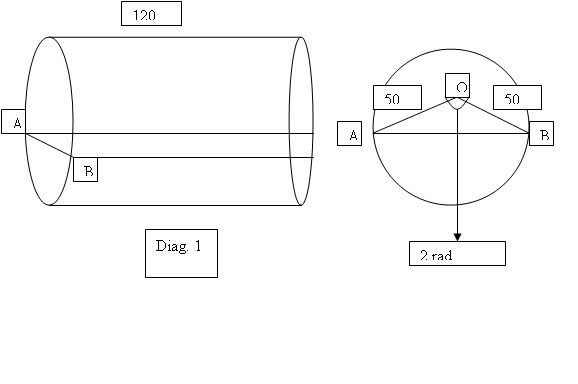
Find the area of the internal surface of the tank which is in contact with the water in diagram 1. Ans:14700 cm2
Can't visualise the diagram 2 really. If someone can, could you help me out with this question. Cant seem to get the answer. Thanks!
-
For diagram 2, imagine you are looking at the cylinder from the front or back.
The answer is correct to 3 significant figures.
In your best interest, I refrained from providing the solution.
-
Arc length area (contact with water) = 2 rad x 50 x 120 = 12000 cm2
the 2 vertical ends = pi x r^2 x (2 rad / 2pi) x 2 = 5000 cm^2
Area of 2 - triangles AOB = 0.5 x 50 x 50 x sin (2 rad) x 2 = 2273 cm^2
So area in contact with water = 12000 + 5000 - 2273
= 14727 cm^2