Trigonometric question (maths)
-
the below question seems flawed. please take a look.
the diagram shows a point A which lies 10 km south of a point B. The points C and D are both 7 km from B and the bearing of C from A is 035 deg. The points A,C,D and E all lies on a straight line. Calculate
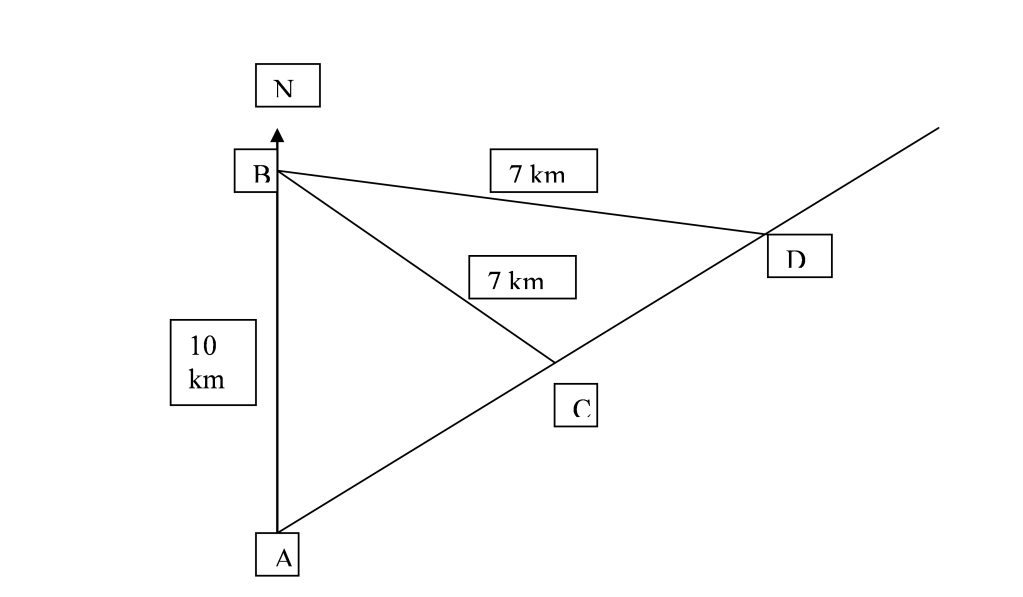
(a) angle ACD (ans:125.0deg)
(b)bearing of C from B (ans:160deg)
(c) the length of CD (8.03cm)
(d) the shortest distance from B to the line ACD (5.73cm)
for (a), I applied the use of sine rule and got something around 55 deg. I proceeded to do (b) which of course gave me a different set of answer from the answer scheme since my answer for (a) is already different from the mark sheet.
To confirm the flaw in this question, I double-checked by doing this
by sine rule, we know that angle ACD is around 55deg. then look again, to find angle BDC, we also use sine rule and again the answer is 55 deg (same as that of angle ACD) however we know that it is wrong because surely BC and BD are not parallel?
Please confirm this for me. Thanks
-
i guess u typed the question for a) incorrectly
125.0° is angle BCDa) sin ACB/10 = sin 35°/7
ACB = 55.0°
BCD = 180° - ACB = 125°if this is true, angle ABC should be 90°, implying that ABC is a right-angled triangle, and hence b) the bearing of C from B should be 90° which does not satisfy the answer provided
-
Better show the folks here the original diagram instead of the one you drawn.
Because if BCD is isosceles,
1) then the perpendicular to the base MUST lie at the midpoint of CD.
2) BCD can't be obtuse as implied by your diagram.
And if A, C and D lies on a staight line, how can ACD be anything other than 180? And where is E?
If your diagram is "accurate", then don't bother to do it as it is flawed.