E maths
-
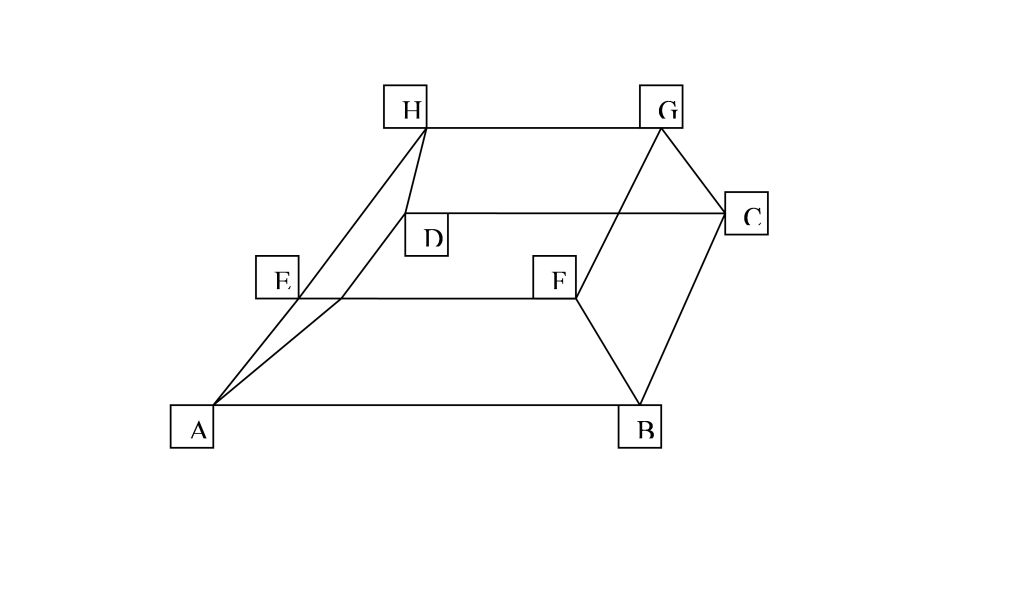
Calculate the volume of the frustum ABCDEFGH shown in the diagram, in which AB = DC = 8 cm, BC = AD = 6 cm, EF = HG = 4cm, FG = EH = 3 cm and the height of the frustum is 5 cm (ANSWER: 140 cm3)
2. ABC is a triangle lying in a HORIZONTAL plane with angle BAC = 90 deg and BC = 22.5 m. V is a point vertically above A and the angles of elevation of V from B and C are 46.6 deg and 40 deg respectively
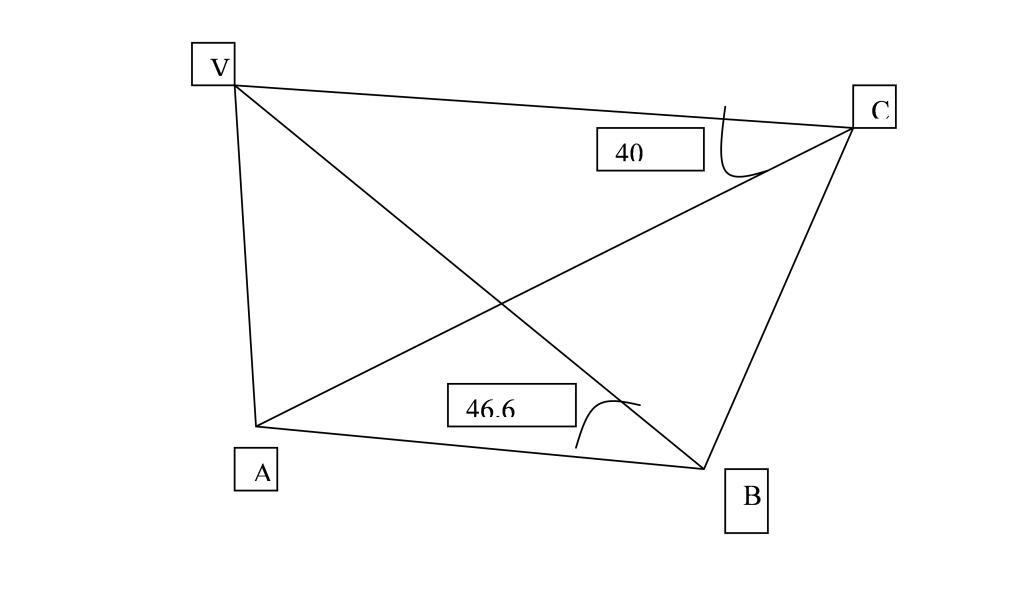
Show that the height of VA is approximately 14.8 m
Thanks
-
I tried working out for part (a) but couldn't get the answer. But anyway, just to give you an idea of how my thinking goes.
As you can see, the frustum is part of a rectangular base of a pyramid. So I "extended" the height of the frustum and let the remaining upper part have a height of x to form a complete pyramid. Next you notice that the upper part of the pyramid is similar to that of the entire pyramid. Perhaps it has something to do with similarity of shapes.
I can't get the answer... but it is something that works along those lines.
-
Originally posted by anpanman:
Calculate the volume of the frustum ABCDEFGH shown in the diagram, in which AB = DC = 8 cm, BC = AD = 6 cm, EF = HG = 4cm, FG = EH = 3 cm and the height of the frustum is 5 cm (ANSWER: 140 cm3)

2. ABC is a triangle lying in a HORIZONTAL plane with angle BAC = 90 deg and BC = 22.5 m. V is a point vertically above A and the angles of elevation of V from B and C are 46.6 deg and 40 deg respectively

Show that the height of VA is approximately 14.8 m
Thanks
1.
Notice that the structure is a shaved off pyramid.
Let mid point of ABCD be X and midpoint of EFGH be Y.
Using similar triangles ( XB and YF ), find the height of the entire pyramid and that of the cut away pyramid.
After doing so, find the volume of the entire pyramid, then find the entire volume of the cut away section.
Use these 2 volumes to find the volume of the frustum.
2.
AC^2 = AB^2 + BC^2
VAB = VAC = 90degrees
VA / sinVBA = AB / sinAVB
AC / sinAVC = AV/ sinVCA
Use all these to find length of VA and area of ABC.
Use these two to find volume via formula pyramid's volume.
-
Originally posted by Forbiddensinner:
1.
Notice that the structure is a shaved off pyramid.
Let mid point of ABCD be X and midpoint of EFGH be Y.
Using similar triangles ( XB and YF ), find the height of the entire pyramid and that of the cut away pyramid.
After doing so, find the volume of the entire pyramid, then find the entire volume of the cut away section.
Use these 2 volumes to find the volume of the frustum.
2.
AC^2 = AB^2 + BC^2
VAB = VAC = 90degrees
VA / sinVBA = AB / sinAVB
AC / sinAVC = AV/ sinVCA
Use all these to find length of VA and area of ABC.
Use these two to find volume via formula pyramid's volume.
AC^2 = AB^2 + BC^2
Is this part wrong? Angle CAB is 90deg so shouldnt BC be the hypotenuse? By the way still can't solve the seond part...Thanks anyway
-
Hi,
Let me clarify further, based on what has been discussed.
We consider the following facts:
1. AC^2 + AB^2 = 22.5^2;
2. Angle VAB = angle VAC = 90 deg;
3. By sine rule in triangle VAB, VA / sin (44.6 deg) = AB / sin (45.6 deg);
4. By sine rule in triangle VAC, VA / sin (40 deg) = AC / sin (50 deg).
Approach: Substitute AB (point 3) and AC (point 4) into the equation in point 1 to find VA.
Nice question!
Thanks!
Cheers,
Wen Shih -
Originally posted by wee_ws:
Hi,
Let me clarify further, based on what has been discussed.
We consider the following facts:
1. AC^2 + AB^2 = 22.5^2;
2. Angle VAB = angle VAC = 90 deg;
3. By sine rule in triangle VAB, VA / sin (44.6 deg) = AB / sin (45.6 deg);
4. By sine rule in triangle VAC, VA / sin (40 deg) = AC / sin (50 deg).
Approach: Substitute AB (point 3) and AC (point 4) into the equation in point 1 to find VA.
Nice question!
Thanks!
Cheers,
Wen ShihThanks for the help!
I was looking at Forbiddensinner's working just now and I realised he mentioned something about finding the volume of the shape. Well, surely we can't find the base area of triangle ABC X VA because this isn't a pyramid whatsoever. Is there anyway we can effectively derive the volume? Thanks again!
-
Hi,
Once VA is found, AB and AC are known.
Then the volume of the pyramid VABC can be determined.
Thanks!
Cheers,
Wen Shih