Plane geo

• anpanman

  5 Oct 09, 21:10

  PQ is a chord of the circle centre O. The tangents at P and Q to the circle meet at X and OX intersects PQ at N. Prove that

  1. Triangle XPO is similar to triangle XNP

  2. ON . OX = OP^2

  

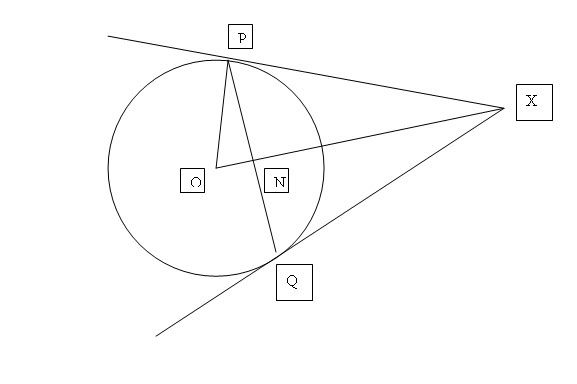
  Tried to prove part 1 using alt. seg. or intersecting chords theorem but realized that both theories can't be applied. Can someone help me out with this?

  Thanks!

• wee_ws

  5 Oct 09, 21:48

  Hi,

    1. angle PXO = angle NXP

    2. angle XPO = angle XNP = 90 degrees

    so by AA, triangle XPO is similar to triangle XNP.

    Thanks!

  Cheers,
  Wen Shih

• TrueHeart

  5 Oct 09, 21:55

  Originally posted by anpanman:

  PQ is a chord of the circle centre O. The tangents at P and Q to the circle meet at X and OX intersects PQ at N. Prove that

  1. Triangle XPO is similar to triangle XNP

  2. ON . OX = OP^2

  

  Tried to prove part 1 using alt. seg. or intersecting chords theorem but realized that both theories can't be applied. Can someone help me out with this?

  Thanks!

  Since Mr Wee has kindly posted up the first part, I will elaborate on the second part. 

  Working from the right side, OP^2 = PN^2 + ON^2 = ON( PN^2/ON + ON ) = ON.OX

  From the 1st part, we know that PN/ON = XN/PN, thus ( PN^2/ON + ON ) = OX

• wee_ws

  5 Oct 09, 22:24

  Hi anpanman,

    In case you get stuck in the first part during the exam, just use the result anyway to do the second part. You'll still score a few marks instead of a zero if you give up the entire question.

    Thanks and jiayou!

  Cheers,
  Wen Shih

• anpanman

  6 Oct 09, 06:09

  Originally posted by wee_ws:

  Hi,

    1. angle PXO = angle NXP

    2. angle XPO = angle XNP = 90 degrees

    so by AA, triangle XPO is similar to triangle XNP.

    Thanks!

  Cheers,
  Wen Shih

  How do you know angle XNP = 90 deg? Thanks!

• wee_ws

  6 Oct 09, 06:20

  Hi,

    Triangle POQ is isosceles. Let angle POQ be theta. Then you should be able to see why. Thanks!

  Cheers,
  Wen Shih

• TrueHeart

  6 Oct 09, 06:24

  Originally posted by anpanman:

  How do you know angle XNP = 90 deg? Thanks!

  Sorry to have extra posted when Mr Wee has already done so.