H2 maths tutor needs help
-
Hi guys, I'm a H2 maths tutor and I need some help.
My student was given the following question last year for her mid-year exams. It's a maxima-minima question.
A piece of wire of length 20 cm is bent to form a figure which comprises a semi-circle with center O and radius x cm and a right-angled isoceles triangle with two equal sides of length y cm as shown in the figure below.
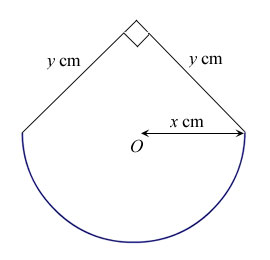
(i) Show that A = ½πx2 + ½(10 – ½πx)2, where A denotes the area enclosed by the figure.
(ii) By differentiation, find the minimum area of A as x varies. Give your answer to the nearest cm2.
The first part of the question is fine, but I am wondering if the second part is flawed. If the perimeter is fixed at 20cm, and the top angle is stipulated to be a right-angle, then it seems that x can no longer vary.
For example, if x becomes smaller, the semi-circle becomes smaller, so the right-angle is forced to become an acute angle, to keep the perimeter fixed at 20cm.
So this is a flawed maxima-minima question? The question doesn't make sense?
I told my student that the question is flawed but I would appreciate a second opinion, just to confirm. Thanks.
-
I can't think of any way x can vary either, according to those restrictions. I think the question is just asking to put dA/dx to 0 and then find A, but phrasing it in a terrible way.
-
Hi Mad Hat,
Part (ii) is alright. With a smaller x, the semicircle portion will look like a major arc instead. Thanks.
Cheers,
Wen Shih -
Very very nice question. Thanks for sharing!
-
Originally posted by wee_ws:
Hi Mad Hat,
Part (ii) is alright. With a smaller x, the semicircle portion will look like a major arc instead. Thanks.
Cheers,
Wen ShihI believe you meant "y".
Because X cannot change unless Y changes due to the "right-angled isoceles triangle."
-
x and y have to change together.
Do not be bogged down by the right angle.
The wire was bent to form that shape, yes, but as x and y varies, there's no need for it to be right angled anymore. The question did not state that it has to remain right angled as x and y varies.
The only thing that will remain constant would be the isoceles triangle and the semi-circle shape. This is because the equation for A was formed on this assumption. Note that A was not formed because of the right angle, but because of the semi-circle shape and the isoceles triangle.
If there's anything wrong with the question, I would say it's the phrase "right angled" that wasn't made clear.
-
Hi,
Yes, x and y change accordingly while the perimeter remains constant at 20cm.
Since 2y + pi x = 20, y increases if x decreases and y decreases if x increases.
When x drops in value and creates a smaller semi-circle, y increases at the same time to maintain the perimeter at 20cm. The structure of a triangular top and semi-circular bottom remains. Please pardon my wrong explanation posted earlier.
Indeed, a good question that encourages reflection and discussion :)
Cheers,
Wen Shih -
Hi everyone, thanks for the comments. I still have a slight worry.
If the triangle need not remain right-angled as x and y vary, isn't there a problem with the given formula for the area A?
Because the formula is just the area sum of the semi-circle + right-angled triangle.
Area semi-circle = ½ π x2Area right-angled triangle
= ½ y2
= ½(10 – ½πx)2 ........... since y = 10 – ½πx.As such, A = ½ π x2 + ½(10 – ½πx)2.
But if the triangle need not remain right-angled as x and y vary, then this formula for A will not apply generally as x and y vary. (It only applies when the triangle is right-angled?) So can we still use it for dA/dx?
-
Hi Mad Hat,
that's a valid point which I didn't consider cuz I didn't work it out :x
It appears to me now that it cannot vary, because the isoceles triangle can be splitted into two more right angled triangles with sides x, x and y (45 degrees)
Solving, we could actually get x = 3.35 and y = 4.74
x could vary if y varies as well, such that the perimeter need not be 20cm, i.e. overlap... But the question wasn't clear. It would be nicer if the question did not specify right angles, such that pygathoras would then be required to find the area of the triangle instead.
I guess at the end of the day, what is going to happen to the shape, x or y, isn't being tested, but the mechanical portion of getting the values out by setting dA/dx = 0. :X
-
Hi,
If we use the general formula for area of a triangle, i.e.,
1/2 y^2 sin \theta
then the angle does not matter. Thanks.
Cheers,
Wen Shih -
Thanks guys, much appreciated. That clears it up for me. So it's probably better if the question didn't mention the right angle and used a more general formula for the area of an isoceles triangle, not necessarily right-angled.
I actually have a few more questions like this one, where I cannot see what the teacher is up to, or have a different answer from the teacher, or sometimes the wording of the question is puzzling.
I will post them up soon. I hope this will be helpful to students as well, to give them some insight into the thinking of the teachers ...
-
No wonder my frenz failed his maths. So hard.
-
Here's another question I have trouble with. It's a probability question from my student's tutorial sheet. My answer differs from the teacher's answer. I don't have direct contact with the teacher so it's hard for me to ask him. Anyway, it's not very nice if I suggest his answer may be wrong

An unbiased die is thrown six times. Calculate the probability that a 6 occurs only on the last throw and that exactly three of the first five throws result in odd numbers.
The teacher's answer is 36 / 625. No working is given but I think his calculation must be this:
5C3 x (3/5)3 x (2/5)2 x 1/6
= 36 / 625This looks natural because, in the first five throws, no 6 is allowed, so only the numbers 1 to 5 are in play. So, for those throws, the chance of an odd number is 3/5 while the chance of an even number is 2/5.
But I wonder if the correct calculation should be this:
5C3 x (3/6)3 x (2/6)2 x 1/6
= 5 / 216Shouldn't the red denominators be 6, not 5, because all the numbers 1 to 6 are actually in play, even on the first five throws? It was my student who spotted this actually, so I must give her credit here.
But I'm not 100% sure because the teacher's answers are usually correct! Which calculation is actually correct?
-
The teacher is wrong. You are correct.
Must know that the teacher is not always correct. Example, a certain JC's notes for vector planes.... They called scalar product form as vector form, and vector form as parametric... That's wrong...
-
Hey eagle, thanks again! I guess the JC teachers are only human. It is useful to have this feeback cos I usually work alone. Be back soon with another query ...
...
-
Back! This question is from the ten-year series, Binomial & Poisson:
At a fire station, each call-out is classified as either genuine or false. Call-outs occur at random times. On average there are two genuine call-outs in a week, and one false call-out in a two-week period.
(i) Calculate the probability that there are fewer than 6 genuine call-outs in a randomly chosen two-week period.There is a part (ii), but that part is okay. The problem is part (i). My answer differs from the TYS answer of 0.440. Is this a typo? (I'm using last year's edition.) My calculation is this:
X = number of genuine call-outs in a two-week period.
X ~ Po(4)
P(X < 6) = e-4(1 + 4 + 42/2! + ... + 45/5!) = 0.785TYS sometimes has typos but you can normally tell it's a typo. This is the only TYS question where I'm not sure if it's a typo. Is my calculation wrong?
I actually have a list of TYS typos if anyone is interested.
-
You should be correct.
The main reason is because the mean is 4, and the greatest probabilities (in a p.d.f.) usually occurs around the mean. Hence, the sum of probabilities from 0 to 5 is very very likely to be greater than 0.5 ==> This is one sanity check I teach my students.
-
I agree the sanity check is good
 If the mean over two weeks is 4 calls, then chances should be fair it will be less than 6. The question is also quite straightforward.
If the mean over two weeks is 4 calls, then chances should be fair it will be less than 6. The question is also quite straightforward.Usually if the TYS answer is wrong, there is a simple explanation, but, in this case, I couldn't find any. I tried different "natural mistakes" to see if I could end up with the TYS answer of 0.440 but couldn't find a way.
Maybe there's a typo in the question !
Mr. Wee (or Dr. Wee) is involved in the TYS right? Hopefully he can confirm. There is actually another TYS question where the given answer made me scratch my head. It's on complex numbers loci. This is more interesting and I will post it soon.
-
Mr Wee is involved only in the DYNA solution guides.
I don't think he will be involved in other guides like SAP.
-
The one I have is the GCE A-level H2 DYNA guide (2009 edition). Yellow cover. Maybe I shouldn't have called it ten-year series. I thought there was only one. Wee Wen Shih is listed as the author. What is SAP?
-
Singapore Asian Publications
-
Dear Mad Hat,
Thanks for being meticulous in checking for typos. Your answer of 0.785 is correct. You may send the list of errors to Dyna Publisher via email for their correction. In the past, I have identified errors in the answers too. You may also send the list to me via PM, so that I could put it up on my website for users of TYS. Acknowledgement will be given :)
Thanks again.
P.S. It is always good for us to teach students how to check their answers, like Eagle's reasonableness check.
Cheers,
Wen Shih -
Hi Mr. Wee, thanks for confirming that question! I have another similar question from the TYS which I will post soon. As for checking for typos, you're welcome. I will PM you a list before long - I'll check the latest DYNA edition first in case some of the typos have already been corrected.
In appreciation for all the help, may I share with everyone the following probability problems, which are simple yet enlightening:
Mr. Lim has two children. At least one of them is a boy. What is the probability that the other one is also a boy?
This is a famous trick question in conditional probability. The natural answer is 1/2 but, surprisingly, the correct answer is 1/3! This is within the H2 syllabus.
But now consider this question:
Mr. Tan has two children. You see him walking with a boy, which, he explains, is his son. (So now you know that at least one of his children is a boy.) What is the probability that the other one is also a boy?
This looks like the same question but, surprisingly, in this case, the answer of 1/2 is perfectly correct! Am I right?

Thankfully, the difference between the two questions is not within the H2 syllabus, but I'll be happy to discuss both problems if anyone is interested.
-
Question 1
Mr. Lim has two children. At least one of them is a boy. What is the probability that the other one is also a boy?
Steps
(1) Given the condition at least one boy (BB, BG, GB) ie (1/2 x 1/2) x 3
(2) So, given the condition that at least one boy, the probability that the other one
is also a boy ie
P(BB)
= -----------------------
P(BB, BG, GB)
1/2 x 1/2
= ----------------------
( 1/2 x 1/2) x 3
= 1/3
Question 2
Mr. Tan has two children. You see him walking with a boy, which, he explains, is his son. (So now you know that at least one of his children is a boy.) What is the probability that the other one is also a boy?
Steps
(1) Given the condition that the first child is already known as a boy ie a
probability of 1
(2) So, given that the condition that the first child is already known as a boy,
the probability that the other boy is also a boy
= 1 x 1/2 (alternatively (1/2) / 1 = 1/2)
= 1/2
PS : By the way, the correct answers for the H2 Maths past years examination questions can be found in the mark schemes provided by the Cambridge Chief examiner and these mark schemes and examiners' reports are sent to the heads of Maths departments of all the JCs and MI in Singapore.
-
Hi,
When I was still teaching in a school, our HOD would pass around the examiners' report for teachers' reference on common mistakes/misconceptions/answers. However, we never had access to the mark scheme from MOE. I wonder if the practice has changed, since I wrote to SEAB, years ago, to give teachers and parents access to mark schemes to increase transparency? This is a standard practice in UK and Australia.
Thanks.
Cheers,
Wen Shih