Sec 3 Maths Challenging Question

• kkhing

  3 Feb 12, 23:40

  Hi,

  Can someone help to solve this sec 3 challenging question? I tried to solve but couldn't get the answer. Thanks. The answer is x~34.3.

  

   

• eagle

  4 Feb 12, 00:45

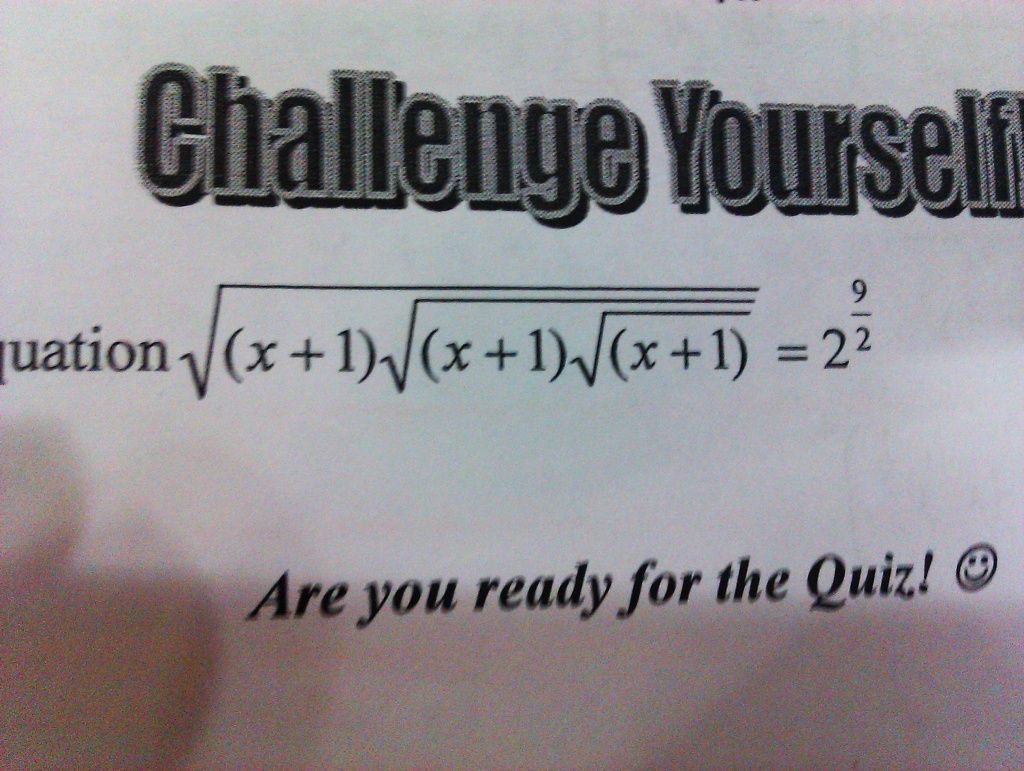
  Why is it challenging?

  Square both sides
  (x+1) sqrt( (x+1) sqrt (x+1) ) = 2^9
  Square both sides again
  (x+1)^2  (x+1) sqrt (x+1) = 2^18
  or
  (x+1)^3 sqrt (x+1) = 2^18
  Square both sides again
  (x+1)^7 = 2^36
  so x+1= 2^ (36/7)
  x = 34.3 (use calculator)

• wee_ws

  4 Feb 12, 05:37

  Hi,

    It is understandably challenging for two reasons:

    1. The form is atypical to the student.

    2. The method of squaring several times is not conventionally applied.

    Thanks.

  Cheers,
  Wen Shih

• frekiwang

  4 Feb 12, 08:37

  let (x+1)=y, we have

  {y[y(y^0.5)]^0.5}^0.5 [y(y^1.5)^0.5]^0.5=[y(y^0.75)]^0.5=(y^1.75)^0.5=y^0.875

  since y^(7/8)=2^(9/2)

  y=2^(9/2)^(8/7)=2^(36/7)=35.33

  x=y-1=34.33

• wee_ws

  4 Feb 12, 20:08

  Hi,

    frekiwang's method is excellent, via substitution and simple use of indices.

    Thanks for sharing!

  Cheers,
  Wen Shih

• eagle

  5 Feb 12, 09:37

  Originally posted by wee_ws:

  Hi,

    It is understandably challenging for two reasons:

    1. The form is atypical to the student.

    2. The method of squaring several times is not conventionally applied.

    Thanks.

  Cheers,
  Wen Shih

  Actually I was waiting for the student to think and understand why it was challenging. :)

  I was thinking if it was a good method to start asking students on why they think certain questions are challenging and difficult, and not simply brush it off as difficult.

   

   

  A more challenging question would be unlimited square rooting. 

  i.e.

  Find the value of sqrt (2 sqrt (2 sqrt (2 sqrt (2 sqrt (2 sqrt (2 sqrt (2 sqrt (2 .........))))))))

  *Changed question*

• wee_ws

  5 Feb 12, 14:32

  Hi eagle,

    Students I have often encountered find thinking hard because they have no structure provided by schools. The usual comments are 'everything is important', 'just use this/that and problem solved' and 'be self-directed'. :P

    Your proposed question can be used as a recurrence question in H2 Maths. I have asked it before in a mock exam I set some years ago :)

  Cheers,
  Wen Shih

   

• StriveOn

  5 Feb 12, 14:49

  Mathematics is like tat one.

  When you dunno, it is like Rocket Science.

  When you know, you wonder why your friend so stupid.

• PhdGuy

  9 Feb 12, 13:39

  Originally posted by frekiwang:

  let (x+1)=y, we have

  {y[y(y^0.5)]^0.5}^0.5 [y(y^1.5)^0.5]^0.5=[y(y^0.75)]^0.5=(y^1.75)^0.5=y^0.875

  since y^(7/8)=2^(9/2)

  y=2^(9/2)^(8/7)=2^(36/7)=35.33

  x=y-1=34.33

  Once again, I am impressed. Are you a student or tutor?

• UltimaOnline

  9 Feb 12, 14:42

  Originally posted by PhdGuy:

  Once again, I am impressed. Are you a student or tutor?

  
  frekiwang is an MOE teacher.